Expression Tree in Data Structure: Properties, Construction with Examples

Expression trees are a primary data structure for representing arithmetic and logical expressions in many notations (infix, postfix, and prefix). Expression trees can represent many kinds of expressions, depending on the operators, operands, and relationships based on the arrangement of the tree. Outlined below are the kinds of expressions that can be represented by expression trees:

1. Arithmetic Expressions

Arithmetic expressions use mathematical operations like addition, subtraction, multiplication, and division and are typically based on numerical values (whether constants or variables).

Expression Tree for 3 + 4 * 2

• Infix: 3 + 4 * 2
• Postfix: 3 4 2 * +
• Prefix: + 3 * 4 2

       +
      / \
     3   *
        / \
       4   2

In this example:

• The root is represented by the plus operator.
• The left child is operand 3.
• In this case, the operands are 4 and 2, and the right child is the multiplication operator (*).

2. Boolean Expressions

Boolean expressions represent logical operations such as AND, OR, NOT, and combinations of these operations. They refer to Boolean variables or constants (true and false).

Expression Tree for A AND B OR C

• Infix: A AND B OR C
• Postfix: A B AND C OR
• Prefix: OR AND A B C

        OR
       /  \
    AND    C
   /  \
  A    B

In this case:

• The root is the OR operator. 
• The left child is an AND operation, with A and B as operands. 
• The right child is operand C. 

3. Relational Expressions

Relational expressions compare two values and are used commonly in conditional expressions based upon relational operators—comparative expressions—like: =, >, <, >=, <=, and !=.

Expression Tree for A > B AND C < D:

• Infix: A > B AND C < D
• Postfix: A B > C D < AND
• Prefix: AND > A B < C D

        AND
       /    \
      >      <
     / \    / \
    A   B   C  D

Here:

• The root is the AND operator.
• The left child is a comparison (>) with operands A and B.
• The right child is a comparison (<) with operands C and D.

4. Conditional Expressions

Conditional expressions are expressions that can be used in a decision-making context, such as in if-else statements or a ternary operator. A common example is the ternary conditional operator (? :)

Expression Tree for x > 10 ? y : z:

• Infix: x > 10 ? y : z
• Postfix: x 10 > y z ? :
• Prefix: ? > x 10 y z

        ?
       /  \
      >    :
    / \   / \
   x  10  y  z

In this case:

• The root is the ternary conditional operator (?).
• The left child is the relational expression x > 10.
• The right child is the conditional operation (:), which accepts operands y and z.

An expression tree can be constructed using infix, prefix, or postfix notations. Let's explain how they are constructed and displayed referring to an example:

       +
      / \
     A   *
        / \
       B   C

Infix Notation

In infix notation, operators are placed between operands. This is the most common way of writing arithmetic expressions.

Construction Process (Infix to Expression Tree)

Step 1: Start with the lowest precedence operator (if multiple operators are present).

Step 2: Make this operator the root of the tree.

Step 3: The left subtree is created from the part of the expression to the left of the operator, and the right subtree is created from the part of the expression to the right of the operator.

Step 4: Recursively apply this process to the left and right subexpressions.

Example: A + B * C

• The  + has a lower precedence than *, so + becomes the root.
• Operand A becomes the left child of +.
• The expression B*C becomes the right subtree. Since * has the highest precedence, it is the root of this subtree, and B and C are its children.

Postfix Notation

In postfix notation, operators are placed after their operands.

Construction Process (Postfix to Expression Tree)

Step 1: Start from the left of the postfix expression and push operands onto a stack.

Step 2: When an operator is encountered, pop the required number of operands (2 for binary operators) from the stack, create a new node for the operator, and make the popped operands its children.

Step 3: Push the new operator node back onto the stack.

Step 4: At the end of the expression, the stack will contain a single node, which is the root of the expression tree.

Example: A B C * +

• Push A, B, and C to the stack.
• Pop B and C, form a node with *, and push it back to the stack.
• Pop A and the * nodes, then add a node with + and push it back into the stack.
• The final stack holds the tree's root.

Prefix Notation

Prefix notation consists of operators coming before their operands.

Construction Process (Prefix to Expression Tree)

Step 1: Start from the right of the prefix expression and push operands onto a stack.

Step 2: When an operator is encountered, pop the required number of operands (2 for binary operators) from the stack, create a new node for the operator, and make the popped operands its children.

Step 3: Push the new operator node back onto the stack.

Step 4: At the end of the expression, the stack will contain a single node, which is the root of the expression tree.

Example: + A * B C

• Push the A, B, and C elements onto the stack.
• Pop the B and C elements off, and make a node containing *, and push that back onto the stack.
• Pop the A element and the * node, make a node containing + and push that back onto the stack.
• The final stack will contain the root of the tree. 

Example	Notation	Example	Expression Tree
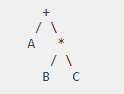	Infix	A + B * C	+ (root), with left child A and right child * (subtree with B and C as leaves)
	Postfix	A B C * +	Same as the infix tree, but the construction order follows postfix operations
	Prefix	+ A * B C	Same as the infix tree, but the construction order follows prefix operations

Here are the advantages and disadvantages of the expression tree:

Advantages

• Expression trees can help to evaluate expressions easily and reliably by methodically applying operators in a structure.
• Expression trees can help condense complex expressions by re-arranging the tree structure.
• Expression trees can also be used for syntax checking (nothing to do with runtime errors that will be highlighted) in compilers - checking for correct grammer of an expression.
• Expression trees are used in many compilers with the goals of optimization through the implementation of algorithms, such as constant folding or common subexpression elimination.

Disadvantages

• The memory footprint of an expression tree can be very large - especially when the expression is very complex.
• Building the expression tree from the expression requires that an expression is parsed which can be time consuming.
• For a simple expression, a tree can be overkill, and direct evaluation may be more efficient.
• With various types of operator, such as unary or ternary, expression trees can be a bit harder to build actually. 

Some of the algorithms are commonly used to manipulate and evaluate expression trees:

• Post-order Traversal: This is a depth-first traversal method used to evaluate expression trees. It processes the left and right subtrees before evaluating the operator at the node.
• Pre-order Traversal: Useful in some cases where we want to print or convert the expression tree to a prefix notation.
• In-order Traversal: In this method, operands are printed in between operators, leading to an infix expression representation.

Expression trees do not only represent mathematical operations; they have been implemented in various programming languages such as C, C++, and Java, to name a few. In fact, these data structures get a lot of attention in compiler design and are used in the evaluation of arithmetic or mathematical expressions. The representation of expressions as a binary tree makes the processes of parsing, evaluation, and optimization (e.g., constant folding and common subexpression elimination) more efficient. 

Implementation in C

Expression trees are typically constructed in C by means of structures for nodes, where every node contains an operator or operand and pointers to its left and right subtrees. The construction is usually done by parsing the postfix (or any other notation) expression and using a stack to create the tree. The code for the structure and the algorithm might look like this:

#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>

// Define tree node
struct Node {
    char data;
    struct Node *left, *right;
};

// Define stack for tree nodes
struct Stack {
    int top;
    unsigned capacity;
    struct Node **array;
};

// Create new tree node
struct Node* newNode(char data) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

// Stack operations
struct Stack* createStack(unsigned capacity) {
    struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
    stack->top = -1;
    stack->capacity = capacity;
    stack->array = (struct Node**)malloc(stack->capacity * sizeof(struct Node*));
    return stack;
}

int isEmpty(struct Stack* stack) {
    return stack->top == -1;
}

void push(struct Stack* stack, struct Node* node) {
    stack->array[++stack->top] = node;
}

struct Node* pop(struct Stack* stack) {
    if (!isEmpty(stack))
        return stack->array[stack->top--];
    return NULL;
}

// Construct expression tree from postfix
struct Node* constructExpressionTree(char postfix[]) {
    struct Stack* stack = createStack(100); // arbitrary capacity

    for (int i = 0; postfix[i] != '\0'; i++) {
        // If operand, create a node and push
        if (isalnum(postfix[i])) {
            push(stack, newNode(postfix[i]));
        }
        // If operator, pop two nodes and make them children
        else {
            struct Node* node = newNode(postfix[i]);

            node->right = pop(stack);
            node->left = pop(stack);

            push(stack, node);
        }
    }

    // Root of the tree
    return pop(stack);
}

// Inorder traversal
void inorder(struct Node* root) {
    if (root != NULL) {
        inorder(root->left);
        printf("%c ", root->data);
        inorder(root->right);
    }
}

// Preorder traversal
void preorder(struct Node* root) {
    if (root != NULL) {
        printf("%c ", root->data);
        preorder(root->left);
        preorder(root->right);
    }
}

// Postorder traversal
void postorder(struct Node* root) {
    if (root != NULL) {
        postorder(root->left);
        postorder(root->right);
        printf("%c ", root->data);
    }
}

int main() {
    char postfix[] = "ab+c*d-";
    struct Node* root = constructExpressionTree(postfix);

    printf("Inorder Traversal   : ");
    inorder(root);
    printf("\n");

    printf("Preorder Traversal  : ");
    preorder(root);
    printf("\n");

    printf("Postorder Traversal : ");
    postorder(root);
    printf("\n");

    return 0;
}

‍

By this method, the system can easily handle the parsing and evaluation of arithmetic expressions. This is one of the ways in which the compiler can be optimized such as constant folding, where the subtrees that represent constant expressions are evaluated at compile time. 

Implementation in C++

An expression tree in C++ is achieved through the use of object-oriented features where nodes and tree operations are encapsulated in classes. The method of construction is similar to C, but it is more readable and maintainable. Here is a short excerpt of the code for illustration:

#include <iostream>
#include <stack>
using namespace std;
// Node class for expression tree
class Node {
public:
char data;
Node* left;
Node* right;
Node(char val) : data(val), left(NULL), right(NULL) {}
};
// Function to construct expression tree from postfix
Node* constructExpressionTree(const string& postfix) {
stack<Node*> st;
for (char ch : postfix) {
// If operand, create a node and push to stack
if (isalnum(ch)) {
st.push(new Node(ch));
}
// If operator, pop two nodes and make them children
else {
Node* node = new Node(ch);
// Right child is the top of stack
node->right = st.top();
st.pop();
// Left child is the next
node->left = st.top();
st.pop();
st.push(node);
}
}
// Final node is root
return st.top();
}
// Inorder traversal (to verify the tree)
void inorder(Node* root) {
if (root != NULL) {
inorder(root->left);
cout << root->data << " ";
inorder(root->right);
}
}
// Preorder traversal
void preorder(Node* root) {
if (root != NULL) {
cout << root->data << " ";
preorder(root->left);
preorder(root->right);
}
}
// Postorder traversal
void postorder(Node* root) {
if (root != NULL) {
postorder(root->left);
postorder(root->right);
cout << root->data << " ";
}
}
int main() {
string postfix = "AB*CD/+";
Node* root = constructExpressionTree(postfix);
cout << "Inorder Traversal : ";
inorder(root);
cout << endl;
cout << "Preorder Traversal : ";
preorder(root);
cout << endl;
cout << "Postorder Traversal : ";
postorder(root);
cout << endl;
return 0;
}

‍

Besides this, C++ expression trees are also a major component of compiler designs used for parsing mathematical expressions and for further stages of compiler like optimization by methods such as common subexpression elimination. 

Implementation in Java

Java provides robust support for building expression trees using classes and data structures such as Stack. Below is an example of constructing an expression tree from a postfix expression:

import java.util.Stack;
class Node {
char data;
Node left, right;
Node(char data) {
this.data = data;
left = right = null;
}
}
public class ExpressionTree {
// Construct Expression Tree from Postfix
public static Node constructTree(String postfix) {
Stack<Node> stack = new Stack<>();
for (char ch : postfix.toCharArray()) {
if (!isOperator(ch)) {
// Operand → create a node and push
stack.push(new Node(ch));
} else {
// Operator → pop two nodes
Node node = new Node(ch);
node.right = stack.pop();
node.left = stack.pop();
stack.push(node);
}
}
return stack.pop();
}
// Check if character is operator
private static boolean isOperator(char ch) {
return ch == '+' || ch == '-' || ch == '*' || ch == '/';
}
// Inorder traversal
public static void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
// Preorder traversal
public static void preorder(Node root) {
if (root != null) {
System.out.print(root.data + " ");
preorder(root.left);
preorder(root.right);
}
}
// Postorder traversal
public static void postorder(Node root) {
if (root != null) {
postorder(root.left);
postorder(root.right);
System.out.print(root.data + " ");
}
}
// Driver Code
public static void main(String[] args) {
String postfix = "AB*CD/+";
Node root = constructTree(postfix);
System.out.print("Inorder Traversal : ");
inorder(root);
System.out.println();
System.out.print("Preorder Traversal : ");
preorder(root);
System.out.println();
System.out.print("Postorder Traversal : ");
postorder(root);
System.out.println();
}
}

Java’s object-oriented features make it convenient to extend expression trees for advanced compiler optimizations or symbolic computation, such as constant folding and detecting common subexpressions.

Output

Infix Expression : a + b * c - d
Prefix Expression : - * + a b c d
Postfix Expression : a b + c * d -

To summarize, an expression tree is a binary tree that represents mathematical expressions in which the leaf nodes are operands and the interior nodes are operators. Expression trees allow for evaluation of an expression while preserving the precedence of operators and for transformations to be simplified. Expression trees are often used in both compilers and calculators in the computer algebra systems for parsing, evaluating or optimizing expressions. Using post-order traversal, arbitrary expressions can be evaluated or simplified quickly.

1. Can an expression tree be utilized to perform symbolic computations?

Yes, expression trees are an important component of symbolic computation systems, allowing for symbolic manipulation and simplification of algebraic expressions.

2. What is the time complexity for evaluating an expression tree?

The time complexity for evaluating an expression tree is O(n), where means the total number of nodes. This is because a post-order traversal processes each node exactly once.